Пересечение произвольной прямой и наклонного эллипса

Тема наклонного эллипса всегда вызывает живой интерес у аудитории. В связи с чем, в этой статье рассмотрим как найти координаты пересечения произвольной прямой и наклонного эллипса.

Предыдущая статья рассказывает, как найти координаты точки на наклонном эллипсе с помощью формул аффинного поворота. В текущей теме, не будучи сильно оригинальными, используем тот же прием. Но несколько в другом ракурсе.

Конечно, можно сделать сложное уравнение повернутого эллипса, и что-то такое вывести. Разместить в рубрике теории и практики. Но если можно сделать проще, понятней и быстрее, то вот честно, лень садиться за блокнот. Тем более что, как показывает практика, никто в теорию не углубляется и вывод формул не смотрит.

Содержание скрыть

Пересечение произвольной линии и эллипса

Формулы аффинного поворота

TPointF в Delphi 7

Рисование наклонного эллипса

Пересечение линии с наклонным эллипсом

Как считать

Комментарии к программе: Анимация

Комментарии к исходнику: TThread

Скачать

Пересечение произвольной линии и эллипса

Есть теоретическая статья на эту тему. Для нахождения координат используется квадратное уравнение. Статья посвящена нахождению коэффициентов этого уравнения.

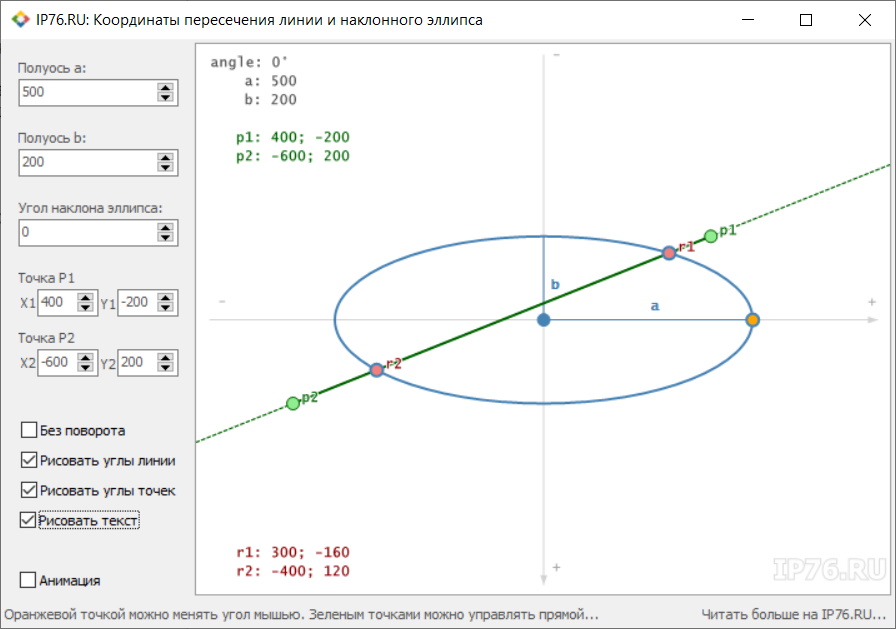
В статье нет исходного кода. Поэтому исправляю ситуацию. Для нахождения координат используется следующая функция.

// Найти координаты точки пересечения прямой (p1, p2) и эллипса
// https://ip76.ru/theory-and-practice/inellipse-line/
function CalcLineInterEllipse(const Rx, Ry: Extended; const p1, p2: TPointF;
  var Res: TRectF): Integer;
var
  k, b, v, s, dx, dy: Extended;
  AA, BB, CC, D: Extended;
begin
  Res := RectF(-1,-1,-1,-1);
  Result := 0;

  dx := p2.x-p1.X;
  dy := p2.y-p1.y;

  if IsZero(dx,0.0001) then
  begin
    AA := 1;
    BB := 0;
    CC := -(1 - (p1.x*p1.x)/(Rx*Rx))*(Ry*Ry);

    D := BB*BB - 4 * AA * CC;
    if D < 0 then
      Exit;

    Res.Left := p1.X;
    Res.Right := p1.X;
    Result := Result + 1;
    Res.Top := (-BB + sqrt(D))/(2*AA);
    if D > 0 then
    begin
      Res.Bottom := (-BB - sqrt(D))/(2*AA);
      Result := Result + 1;
    end;
  end else
  begin
    k := dy/dx;
    b := p1.Y - k * p1.X;
    v := Rx*Rx * Ry*Ry;
    S := b;
    AA := Ry*Ry + Rx*Rx*k*k;
    BB := 2 * (Rx*Rx * k * S);
    CC := Rx*Rx * S*S - V;

    D := BB*BB - 4 * AA * CC;
    if D < 0 then
      Exit;

    Res.Left := (-BB + sqrt(D))/(2*AA);
    Res.Top := Res.Left * k + b;
    Result := Result + 1;

    if D > 0 then
    begin
      Res.Right := (-BB - sqrt(D))/(2*AA);
      Res.Bottom := Res.Right * k + b;
      Result := Result + 1;
    end;
  end;
end;

// Найти координаты точки пересечения прямой (p1, p2) и эллипса

// https://ip76.ru/theory-and-practice/inellipse-line/

function CalcLineInterEllipse(const Rx, Ry: Extended; const p1, p2: TPointF;

var Res: TRectF): Integer;

var

k, b, v, s, dx, dy: Extended;

AA, BB, CC, D: Extended;

begin

Res := RectF(-1,-1,-1,-1);

Result := 0;

dx := p2.x-p1.X;

dy := p2.y-p1.y;

if IsZero(dx,0.0001) then

begin

AA := 1;

BB := 0;

CC := -(1 - (p1.x*p1.x)/(Rx*Rx))*(Ry*Ry);

D := BB*BB - 4 * AA * CC;

if D < 0 then

Exit;

Res.Left := p1.X;

Res.Right := p1.X;

Result := Result + 1;

Res.Top := (-BB + sqrt(D))/(2*AA);

if D > 0 then

begin

Res.Bottom := (-BB - sqrt(D))/(2*AA);

Result := Result + 1;

end;

end else

begin

k := dy/dx;

b := p1.Y - k * p1.X;

v := Rx*Rx * Ry*Ry;

S := b;

AA := Ry*Ry + Rx*Rx*k*k;

BB := 2 * (Rx*Rx * k * S);

CC := Rx*Rx * S*S - V;

D := BB*BB - 4 * AA * CC;

if D < 0 then

Exit;

Res.Left := (-BB + sqrt(D))/(2*AA);

Res.Top := Res.Left * k + b;

Result := Result + 1;

if D > 0 then

begin

Res.Right := (-BB - sqrt(D))/(2*AA);

Res.Bottom := Res.Right * k + b;

Result := Result + 1;

end;

Как говорится в таких случаях, орфография и стилистика в именах переменных сохранены. Результат, равный 0, означает, что пересечений нет, 1 означает, что линия соприкасается с эллипсом в точке Res.TopLeft, 2 — две точки пересечения Res.TopLeft и Res.BottomRight.

Формулы аффинного поворота

Напомню формулы аффинного поворота:

$\displaystyle x'=x \times \cos \alpha-y\times \sin \alpha$

$\displaystyle y'=x \times \sin \alpha+y \times \cos \alpha$

Операция нахождения синуса и косинуса достаточно ресурсоемкая. Поэтому желательно находить их как можно реже. В связи с чем, пишем функцию сразу для двух точек. Почему именно для двух, будет расшифровано в дальнейшем. Можно вообще передавать и возвращать массив точек. Просто тут нам массивы не понадобятся.

// применить аффинное преобразование поворота к двум точкам
procedure RotateTwoPoint(const Angle: Extended; const p1, p2: TPointF;
  var r1, r2: TPointF);
var
  sn, cs: extended;
begin
  SinCos(Angle * PI/180, sn, cs);
  r1 :=  PointF(p1.X * cs - p1.Y * sn, p1.X * sn + p1.Y * cs);
  r2 :=  PointF(p2.X * cs - p2.Y * sn, p2.X * sn + p2.Y * cs);
end;

// применить аффинное преобразование поворота к двум точкам

procedure RotateTwoPoint(const Angle: Extended; const p1, p2: TPointF;

var r1, r2: TPointF);

var

sn, cs: extended;

begin

SinCos(Angle * PI/180, sn, cs);

r1 := PointF(p1.X * cs - p1.Y * sn, p1.X * sn + p1.Y * cs);

r2 := PointF(p2.X * cs - p2.Y * sn, p2.X * sn + p2.Y * cs);

end;

TPointF в Delphi 7

Чтобы использовать тип TPointF в Delphi 7 и функции с ним связанные необходим модуль IP76DrawUtils из исходников в конце статьи. Он также обеспечивает совместимость с XE 7, XE 10, XE 11. На других XE возможности протестировать нет.

Рисование наклонного эллипса

Теоретическая часть, как рисовать эллипс под углом и функция рисования находятся тут.

Пересечение линии с наклонным эллипсом

Что будет, если мы вначале повернем линию на угол, обратный повороту эллипса, а потом повернем эллипс вместе с линией на этот угол? А будет идеальное решение:

Рис.2. Процесс расчета координат пересечения произвольной линии и наклонного эллипса

Как считать

Задать линию можно кучей разных способов. Выбираем способ по двум точкам. Потому что у нас уже есть функция для не-повернутого эллипса, где линия задается как раз парой точек.

Таким образом, алгоритм состоит из трех пунктов:

Повернуть точки p1 и p2, задающие линию, на угол, обратный поворотному для эллипса. Для этого применяются формулы аффинного поворота. Таким образом, получаем точки p1′ и p2′.
Найти точки пересечения линии (p1′, p2′) с не-повернутым эллипсом с помощью квадратного уравнения. Пусть это будут точки r1′ и r2′.
Повернуть точки r1′ и r2′ на угол поворота эллипса. Полученные точки r1, r2 и будут являться результатом.

Собственно, поэтому у нас функция аффинного поворота RotateTwoPoint принимает и возвращает две точки.

Функция расчета:

// Посчитать координаты (AP1, AP2) пересечения линии (ALinePoint1, ALinePoint2)
// с наклонным эллипсом с полуосями A, B под углом Angle (градусы)
// ALineRotP1, ALineRotP1 - повернутые координаты исходной линии
// Результат: 0 - нет пересечений, 1 - линия касается эллипс в точке AP1
//   2 - пересечение в точках AP1, AP2
function CalcCoordIntersectLineEllipse(const A, B, Angle: Extended;
  const ALinePoint1, ALinePoint2: TPointF;
  var ALineRotP1, ALineRotP2, AP1, AP2: TPointF): Integer;
var
  CalcRect: TRectF; // пересечение линии с не-повернутым эллипсом
begin
  // 1. Аффинный поворот на угол, обратный заданному
  RotateTwoPoint(-Angle, ALinePoint1, ALinePoint2, ALineRotP1, ALineRotP2);
  // 2. Пересечение повернутой линии с не-повернутым эллипсом
  Result := CalcLineInterEllipse(A,B, ALineRotP1, ALineRotP2, CalcRect);
  // 3. Аффинный поворот найденных точек пересчения на заданный угол
  if Result > 0 then
    RotateTwoPoint(Angle, CalcRect.TopLeft, CalcRect.BottomRight, AP1, AP2);
end;

// Посчитать координаты (AP1, AP2) пересечения линии (ALinePoint1, ALinePoint2)

// с наклонным эллипсом с полуосями A, B под углом Angle (градусы)

// ALineRotP1, ALineRotP1 - повернутые координаты исходной линии

// Результат: 0 - нет пересечений, 1 - линия касается эллипс в точке AP1

// 2 - пересечение в точках AP1, AP2

function CalcCoordIntersectLineEllipse(const A, B, Angle: Extended;

const ALinePoint1, ALinePoint2: TPointF;

var ALineRotP1, ALineRotP2, AP1, AP2: TPointF): Integer;

var

CalcRect: TRectF; // пересечение линии с не-повернутым эллипсом

begin

// 1. Аффинный поворот на угол, обратный заданному

RotateTwoPoint(-Angle, ALinePoint1, ALinePoint2, ALineRotP1, ALineRotP2);

// 2. Пересечение повернутой линии с не-повернутым эллипсом

Result := CalcLineInterEllipse(A,B, ALineRotP1, ALineRotP2, CalcRect);

// 3. Аффинный поворот найденных точек пересчения на заданный угол

if Result > 0 then

RotateTwoPoint(Angle, CalcRect.TopLeft, CalcRect.BottomRight, AP1, AP2);

end;

Комментарии к программе: Анимация

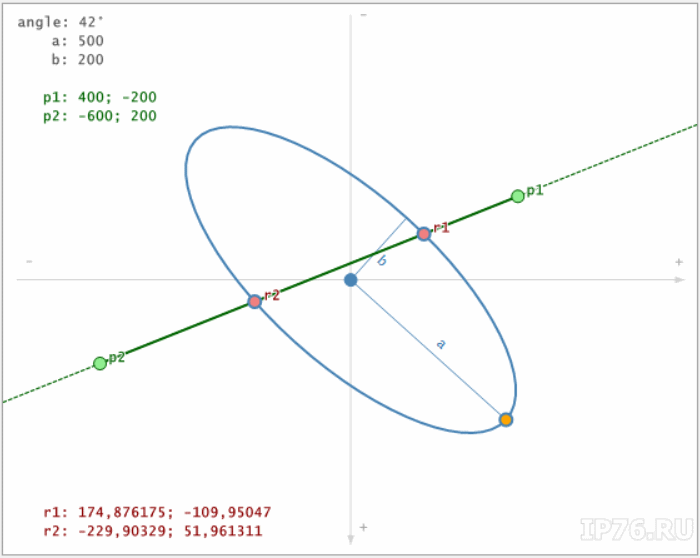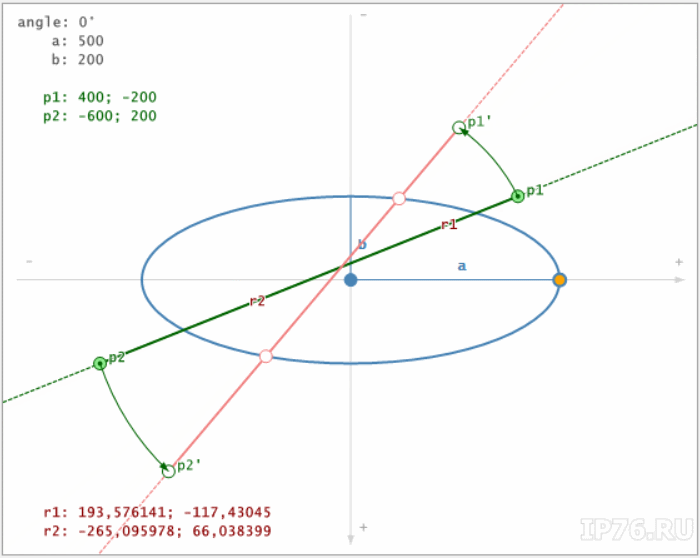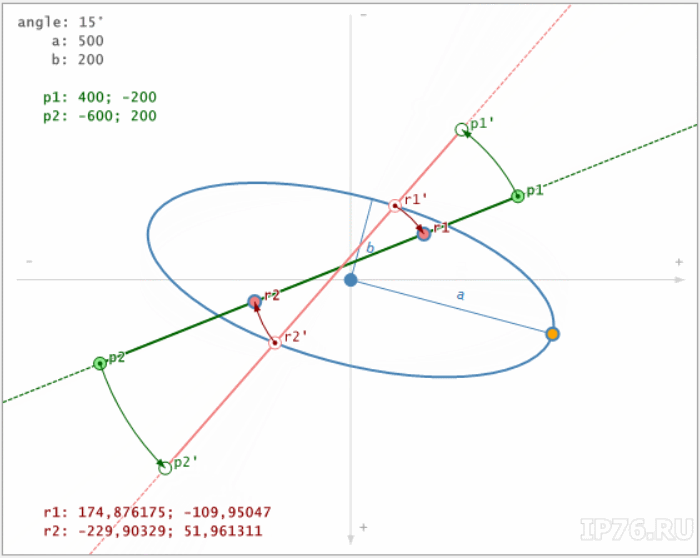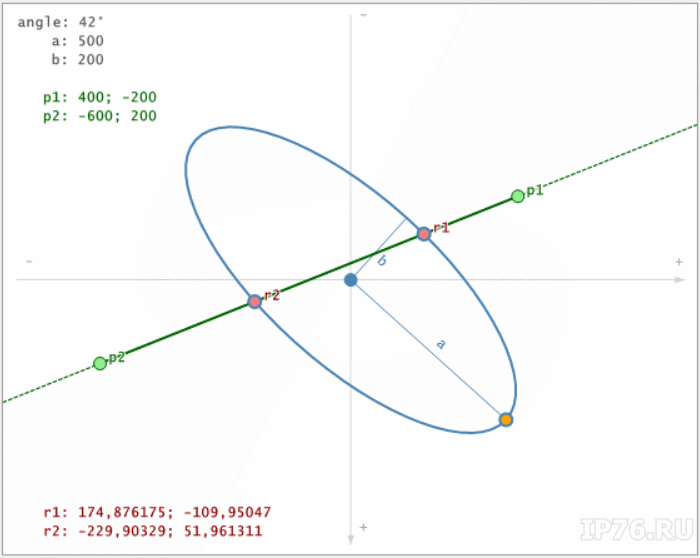
Чтобы увидеть, как происходить расчет, со всеми углами и подписями, надо вначале выставить все галки, как на рисунке 3, и повернуть эллипс на желаемый угол.

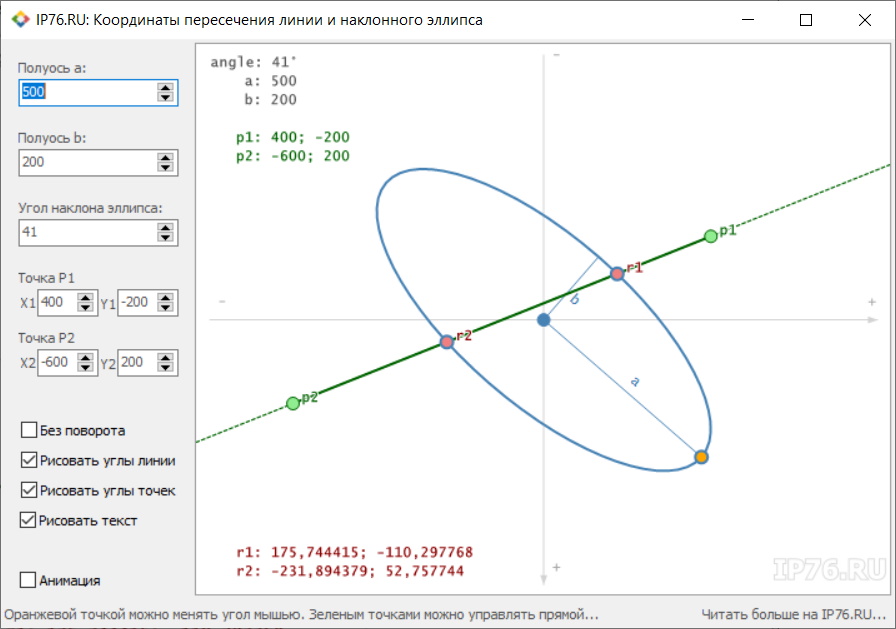
После этого поставить галку в «Анимации». Будет происходить действо, как на рисунке 2. Можно поиграться с галкой «Без поворота», но боюсь данное действие может немного запутать кучей линий на экране.

Комментарии к исходнику: TThread

Внутри, конечно, много интересного. Но меня периодически спрашивают, почему я не использую потоки (которые нити) для анимации и как использовать класс TThread. Поэтому в исходнике есть поток:

type
  TAnimThread = class(TThread)

1 2	type TAnimThread = class(TThread)

Он простенький, однако принцип работы демонстрирует. Для работы с полями и компонентами формы используется метод Synchronize. Это не единственный способ работать с чем-то вне потока, но здесь так. Потому что статья не про потоки )))

От себя скажу следующее. По моему мнению, если можно обойтись таймером, то надо обходиться таймером. Для задачи анимации в этой и подобных задачах поток не нужен, потому что все равно основное действо происходит в главном потоке программы. Вот если все расчеты и отрисовку унести в поток — это другое дело.

Скачать

Друзья, спасибо за внимание!

Исходник (zip) 181 Кб. Delphi 7, XE 7, XE 10, XE 11

Для XE открываем файл .dpr и в обязательном порядке build’им.

Пустой подкаталог _dcu в архиве — для Delphi 7.

Исполняемый файл (zip) 296 Кб.

Друзья! Буду чрезвычайно признателен за комментарии, регистрацию на сайте, подписку в телеге. Это очень значимая моральная поддержка для меня.

5 7 голоса

Рейтинг статьи

2 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии

Oleg

Участник

2 лет назад

Пример шикарный, детально описанный в статье и как всегда хорошо документированный в исходниках! Благодарю!

Последний раз редактировалось 2 лет назад Oleg ем

Ответить

Roman

Автор

Ответить на Oleg

2 лет назад

Олег, спасибо! Приятно слышать )))

Ответить