Эллипс под углом и координаты точки наклонного эллипса

С разной периодичностью меня спрашивают о том, как нарисовать эллипс под углом и найти координаты точки наклонного эллипса. Также, участились запросы к сайту на аналогичную тему. Видимо, пора разобраться с этим вопросом.

Содержание скрыть

Эллипс под углом

Если угол от полуоси a

Угол точки от оси X

Как использовать результат

Если центр эллипса не нулевой

Скачать

Эллипс под углом

Ничего более подходящего, чем аффинные преобразования, человечество для этих целей еще не придумало. Аффинные трансформации подвергают все точки плоскости единому преобразованию. В нашем случае, это будет композиция преобразований поворота и переноса.

Как поворачивать разнообразные фигуры можно посмотреть в статье «Как повернуть изображение. GDI, GDI+, Direct2D, JavaScript». Вместо изображения надо просто нарисовать эллипс. Будет ровно тот же эффект.

В нашем случае будем использовать GDIPlus. Чтобы нарисовать эллипс под углом предлагается следующий код.

// Нарисовать эллипс под углом
function DrawRotateEllipse(
  const ACanvas: TGPGraphics; // холст GDI+
  const ARect: TRectF; // область рисования
  const A, B: Single;  // полуоси в экранных координатах
  const Angle: Single  // угол поворота
  ): Boolean;
var
  center: TPointF; // центр области рисования
  pen: TGPPen;     // перо GDI+
  rct: TRectF;     // прямоугольник эллипса
begin
  Result := Assigned(ACanvas);
  if not Result then
    Exit;

  rct := ARect;
  center := CenterRect(rct);

  rct.Left := center.X - A;
  rct.Right := center.X + A;

  rct.Top := center.Y - B;
  rct.Bottom := center.Y + B;

  pen := TGPPen.Create(aclSteelBlue, 2);

  try
    // перенос точки вращения
    ACanvas.TranslateTransform(center.x, center.y);
    // преобразование поворота
    ACanvas.RotateTransform(Angle);
    // обратный перенос
    ACanvas.TranslateTransform(-center.x, -center.y);
    // рисуем как обычный эллипс
    ACanvas.DrawEllipse(pen, rct.Left, rct.Top,
      WidthRect(rct), HeightRect(rct));

  finally
    // обязательный сброс всех трансформаций
    ACanvas.ResetTransform;
    FreeAndNil(pen);
  end;
end;

// Нарисовать эллипс под углом

function DrawRotateEllipse(

const ACanvas: TGPGraphics; // холст GDI+

const ARect: TRectF; // область рисования

const A, B: Single; // полуоси в экранных координатах

const Angle: Single // угол поворота

): Boolean;

var

center: TPointF; // центр области рисования

pen: TGPPen; // перо GDI+

rct: TRectF; // прямоугольник эллипса

begin

Result := Assigned(ACanvas);

if not Result then

Exit;

rct := ARect;

center := CenterRect(rct);

rct.Left := center.X - A;

rct.Right := center.X + A;

rct.Top := center.Y - B;

rct.Bottom := center.Y + B;

pen := TGPPen.Create(aclSteelBlue, 2);

try

// перенос точки вращения

ACanvas.TranslateTransform(center.x, center.y);

// преобразование поворота

ACanvas.RotateTransform(Angle);

// обратный перенос

ACanvas.TranslateTransform(-center.x, -center.y);

// рисуем как обычный эллипс

ACanvas.DrawEllipse(pen, rct.Left, rct.Top,

WidthRect(rct), HeightRect(rct));

finally

// обязательный сброс всех трансформаций

ACanvas.ResetTransform;

FreeAndNil(pen);

end;

Он немного отличается от представленного в статье метода. Там используется класс TGPMatrix. Здесь происходит обращение напрямую к методам холста TGPGraphics. Не смотря на небольшие отличия, принцип абсолютно такой же.

Рис.1. Эллипс под углом 51 град. Полуось a=5, полуось b=2.

В статье «Вращение прямоугольника вокруг произвольной точки» рассматривается метод, как производить поворот вокруг любой точки. Описанный в статье способ можно смело применять к рисованию эллипса.

В интерфейсе проекта по ссылке в конце статьи за оранжевую точку можно вращать эллипс мышкой.

Если угол от полуоси a

Ранее, в этой статье, было расписано, как найти координаты точки эллипса по углу. Вкратце напомню. Там мы находили параметр через арктангенс, который затем использовали в параметрическом уравнении эллипса.

Рис.2. Координаты точки эллипса, отстоящей на 15 градусов от полуоси a.

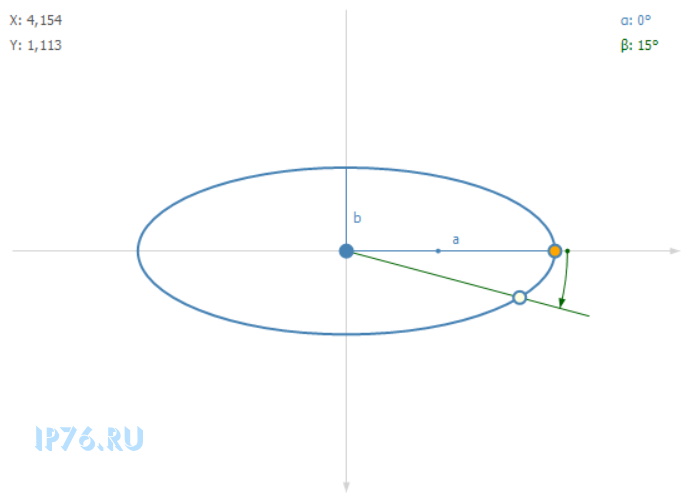
Теперь представим аффинное преобразование. Ко всем точкам плоскости, в том числе и точкам эллипса, применяется одно и то же преобразование. Следовательно, применяя аффинное преобразование поворота к найденным координатам точки, мы получим новые координаты для эллипса под углом.

Подсмотрим в справочнике аффинную матрицу поворота:

$\displaystyle x'=x \times \cos \alpha-y\times \sin \alpha$

$\displaystyle y'=x \times \sin \alpha+y \times \cos \alpha$

Применив дополнительно эти расчеты к полученным координатам видим следующее:

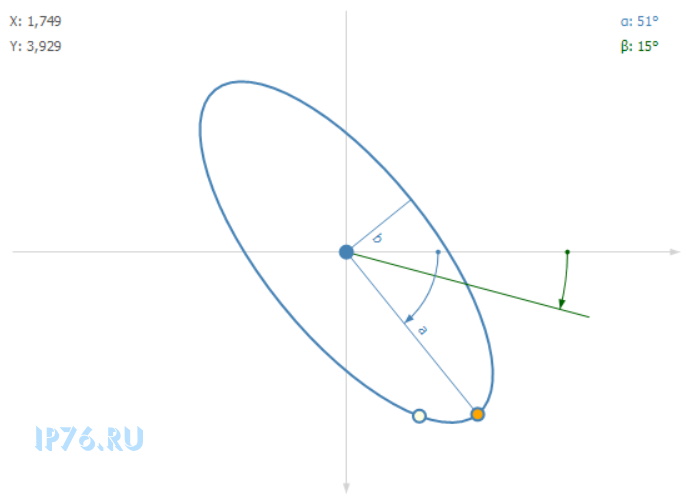
Рис.3. Координаты точки эллипса, повернутого на 51 градус, отстоящей на 15 градусов от полуоси a.

Видим, что точка по прежнему лежит на эллипсе, и реально отстоит от полуоси a на 15 градусов.

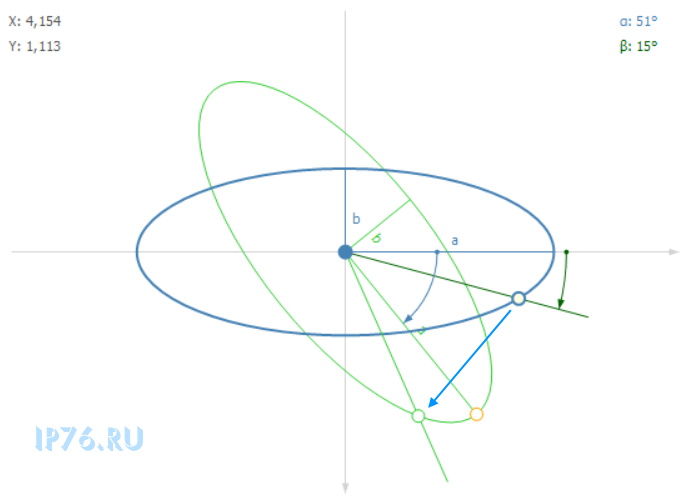
Но в жизни требуется все таки искать координаты точки эллипса, отстоящей на определенный угол от оси X.

Угол точки от оси X

Имеется ввиду следующее:

Рис.5. Координаты точки эллипса, повернутого на 51 градус, отстоящей на 15 градусов от полуоси X.

Как мы уже убедились из предыдущего пункта, формулы аффинного преобразования однозначно переводят точку эллипса в точку эллипса под углом. При этом сохраняется угол между прямой, проведенной из центра через точку P и полуосью a. Теперь задача состоит в том, чтобы найти такую точку P’ на эллипсе, которая при повороте эллипса будет отстоять от оси X на заданный угол.

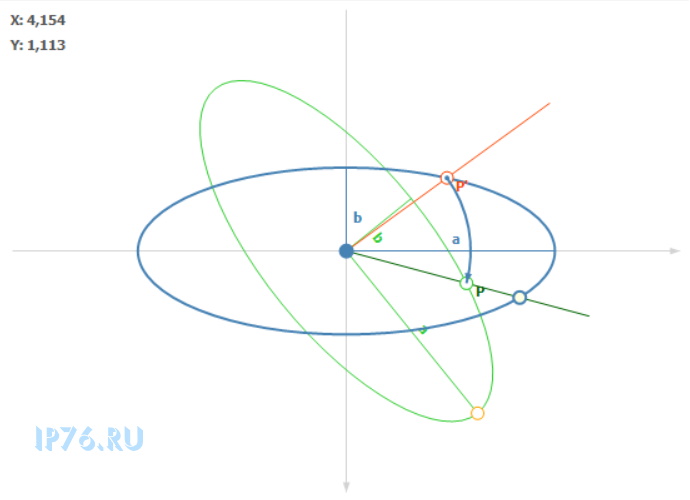
Рис.6. При повороте эллипса точка P’ переходит в точку P, отстоящей от оси X на 15 градусов

Для этого необходимо рассчитать новый угол для этой точки. Этот угол высчитывается очевидным образом как:

γ (Расчетный угол) = β (Угол точки) — ⍺ (Угол поворота)

Рис.7. Расчет угла, для которого находятся координаты точки наклонного эллипса

В итоге, порядок действий таков:

Находим угол для не-повернутого эллипса, который будет соответствовать точке повернутого эллипса, как разность требуемого угла для точки и угла поворота эллипса.
Считаем координаты для этого угла, через нахождение параметра, с дальнейшей подстановкой в параметрическое уравнение эллипса.
К найденным координатам применяем аффинное преобразование поворота.

В коде это выглядит так:

// Посчитать точку на наклонном эллипсе
// A, B - полуоси в реальных координатах
// EllipseAngle - угол поворота эллипса
// Angle  - угол точки
// AFromX - угол от оси X
function CalcEllipsePoint(const A, B, EllipseAngle, Angle: Single;
  const AFromX: Boolean = True): TPointF;
var
  sn,cs: Extended;// синус/косинус
  pnt: TPointF;   // промежуточный результат
  t: Extended;    // угол для расчета параметра/параметр для уравнения
begin
  // посчитать угол
  t := Angle;
  if AFromX then
    t := Angle - EllipseAngle;

  // параметр для уравнения
  SinCos(t * PI/180, sn, cs);
  t := ArcTan2(A * sn, B * cs);

  // координаты точки по параметрическому уравнению
  SinCos(t, sn, cs);
  pnt.X := A * cs;
  pnt.Y := B * sn;

  // аффинное преобразование поворота
  SinCos(EllipseAngle * PI/180, sn, cs);
  result.X := pnt.X * cs - pnt.Y * sn;
  result.Y := pnt.X * sn + pnt.Y * cs;
end;

// Посчитать точку на наклонном эллипсе

// A, B - полуоси в реальных координатах

// EllipseAngle - угол поворота эллипса

// Angle - угол точки

// AFromX - угол от оси X

function CalcEllipsePoint(const A, B, EllipseAngle, Angle: Single;

const AFromX: Boolean = True): TPointF;

var

sn,cs: Extended;// синус/косинус

pnt: TPointF; // промежуточный результат

t: Extended; // угол для расчета параметра/параметр для уравнения

begin

// посчитать угол

t := Angle;

if AFromX then

t := Angle - EllipseAngle;

// параметр для уравнения

SinCos(t * PI/180, sn, cs);

t := ArcTan2(A * sn, B * cs);

// координаты точки по параметрическому уравнению

SinCos(t, sn, cs);

pnt.X := A * cs;

pnt.Y := B * sn;

// аффинное преобразование поворота

SinCos(EllipseAngle * PI/180, sn, cs);

result.X := pnt.X * cs - pnt.Y * sn;

result.Y := pnt.X * sn + pnt.Y * cs;

end;

Как использовать результат

Очевидно, что полученные координаты актуальны для нулевого центра эллипса и реальных размеров полуосей а и b. Как отобразить точку на экране?

У нас есть центр эллипса в экранных координатах FCenter и коэффициент масштаба FScale. Как он вычисляется можно посмотреть в исходниках по ссылке ниже. Экранные координата точки эллипса под углом вычисляются так:

      // 6. Преобразовать FPoint в экранные координаты
      FCalcPoint := PointF(FCenter.X + FPoint.X*FScale,
        FCenter.Y + FPoint.Y*FScale);

// 6. Преобразовать FPoint в экранные координаты

FCalcPoint := PointF(FCenter.X + FPoint.X*FScale,

FCenter.Y + FPoint.Y*FScale);

Если центр эллипса не нулевой

В этом случае надо просто к полученным координатам прибавить координаты центра эллипса.

Скачать

Друзья, спасибо за внимание!

Исходник (zip) 176 Кб. Delphi 7, XE 7, XE 10, XE 11

Для XE открываем файл .dpr и спокойно build’им.

Пустой подкаталог _dcu в архиве — для Delphi 7.

Исполняемый файл (zip) 292 Кб.

Буду чрезвычайно признателен за комментарии, подписку в телеграме и поддержку.

5 8 голоса

Рейтинг статьи

2 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии

Олег

2 лет назад

Огромный Респект, Роман! Очень практичная статья, такая тема остается актуальной в моей работе. На выходных почитаю внимательнее и разберусь с исходниками.

Ответить

Roman

Автор

Ответить на Олег

2 лет назад

Привет, Олег! Спасибо! Будут вопросы по исходникам, комментарь, отвечу. Специально писалось в Delphi 7. Ибо имя им легион. Компилится везде.

Ответить